Introduction.

Hey Guys, today we are going to break our routine where we always speak about life experience and get back to the technical stuffs here. We are going to discuss a common subject in software engineering that any engineer should know about for many reasons. As a software engineer, you will need to know this approach to understand how to design and solve some sort of problems using divide and conquer method, you will need to know that approach to write elegant and simple code to solve complex problems, you will need to know that concept to pass some phone screen interviews and some coding sessions interviews. The concept I’m talking about is recursion.

Recursion principles.

Recursion is a popular concept in the world of software programming. Recursion is a concept of solving problems using a function that calls itself as a subroutine. Yes, you heard it well, a function can call itself, in that situation we are recurring. In a live situation, when a function calls itself, this can continue until a point where the function can not call itself anymore because we reach a base case or because we reach a point where the allocated memory buffer for call function overflowed. In this later case, we are in Stack Overflow situation and your program crashes. So a recursive function should have the following properties so that it does not result in a infinite loop:

• A simple base case (or many base cases) : this is the termination scenario that does not use a recursion to return a result
• A set of rules, also known as a recurrence relation, that reduces other cases towards the base case.

Let's show some examples of recursion functions:

Reverse a string

    class Solution {
        public void reverseString(char[] s) {
            reverseStringHelper(s, 0, s.length - 1);
        }
        public void reverseStringHelper(char[] s, int left, int right) {
            if (left > right) return;
            reverseStringHelper(s, left+1, right-1);
            char temp = s[left];
            s[left] = s[right];
            s[right] = temp;
        }
    }

Swap nodes in pairs

    class Solution {
        public ListNode swapPairs(ListNode head) {
            if (head == null || head.next == null) {
                return head;
            }
            swapPairs(head.next.next);
            int temp = head.val;
            head.val = head.next.val;
            head.next.val = temp;
            return head;
        }
    }

Recurrence relation.

Whenever you have to implement a recursive function, always think about two things that you need to figure out: the base case and the recurrence relation.

• Base case: This is the case where one can compute the answer directly. In the base you just return the answer for the basic situation like if there was no recursion.
• Recurrence relation: This is the relationship between the result of a problem and the result of the sub-problem, given that in the recursion, we are just subdividing the problem into sub-problems. Each recursion represents a sub-problem.

Illustration with Pascal triangle

Let explain the recurrence relation with the example of Pascal triangle. You can have more details about Pascal triangle here

Pascal's triangle is a series of numbers arranged in the shape of triangle. In Pascal's triangle, the leftmost and the rightmost numbers of each row are always 1. For the rest, each number is the sum of the two numbers directly above it in the previous row.

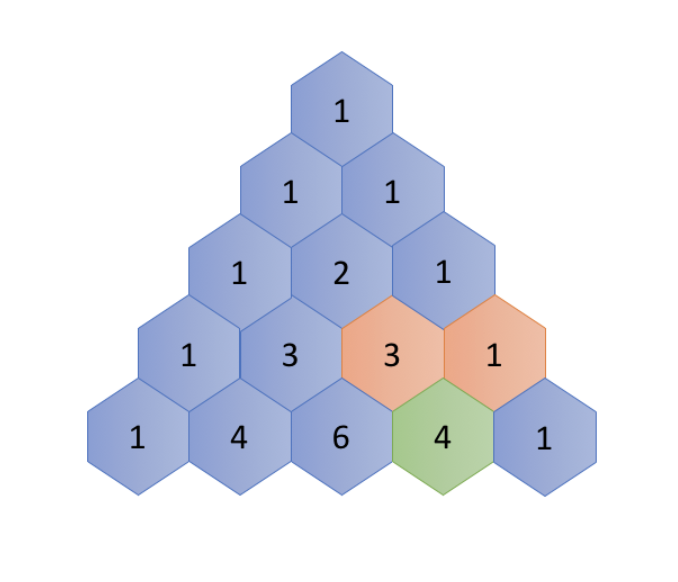
Base case

As we can see, in each line in the Pascal triangle, the leftmost element and the rightmost element are always equal to 1. How can we translate that into a base case rule? We can define the base case as follows : f(i,j)=1, where j=1 or j=i

Recurrence relation

First, we define a function f(i,j) which returns the number in the Pascal triangle in the i-th row and the j-th column.
We then can represent the recurrence relation with the following formula: f(i,j) = f(i−1,j−1) + f(i−1,j)

Demo

Let try to calculate f(5, 3). f(5,3) = f(4,2) + f(4,3), we then call f(4, 2) and f(4, 3) recursively:

• For the call of f(4, 2), we could extend it further until we reach the base cases, as follows :
  f(4, 2) = f(3, 1) + f(3, 2) = f(3, 1) + (f(2, 1) + f(2, 2)) = 1 + (1 + 1) = 3
• For the call of f(4, 3), similarly we break it down as :
  f(4, 3) = f(3, 2) + f(3, 3) = (f(2, 1) + f(2, 2)) + f(3, 3) = (1 + 1) + 1 = 3
• Finally, we combine the results of the above sub-problems: f(5, 3) = f(4, 2) + f(4, 3) = 3 + 3 = 6

Example of code to illustrate the recursion with Pascal triangle

Return the i-th line of the Pascal triangle

    class Solution {
        public List<Integer> getRow(int rowIndex) {
            // Base case
            if (rowIndex == 0) {
                return Arrays.asList(1);
            }
            if (rowIndex == 1) {
                return Arrays.asList(1,1);
            }

            //Recurrence relation
            List<Integer> inter = getRow(rowIndex - 1);
            ArrayList<Integer> result = new ArrayList<>(Arrays.asList(1));
            for (int i = 0; i < inter.size() - 1; i++) {
                result.add(inter.get(i) + inter.get(i+1));
            }
            result.add(1);

            // Returning result
            return result;
        }
    }

In the above demo, we noticed that there are couple of values that are calculated more than one time. When we are doing this, we are wasting time. Later in this article, we are going to see how we can leverage that advantage of already calculated item to improve performance of our algorithm.

Memoization

Memoization is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again. (Source: wikipedia)

Memoization is all about storing the result of pre-calculation in order to reuse them in the future calculation if we need to. This can considerably increase the performance of the algorithm, but in the other hand we have to sacrifice some space to store those results.

To illustrate, let consider the famous Fibonacci series. It is given by the following formula:
F(n) = F(n - 1) + F(n - 2) with the base cases: F(0) = 0, F(1) = 1. The simple code that can solve this problem is the following:

    public int fibonacci(int n) {
        if (n < 2) {
            return n;
        } else {
            return fibonacci(n-1) + fibonacci(n-2);
        }
    }

Let suppose that we want to calculate F(4). F(4) = F(3) + F(2) = (F(2) + F(1)) + F(2). As you can see, in order to obtain the result for F(4), we would need to calculate the number F(2) twice following the above deduction: the first time in the first extension of F(4) and the second time for the intermediate result F(3). Please look at the image below to visualize the duplicate calculations.

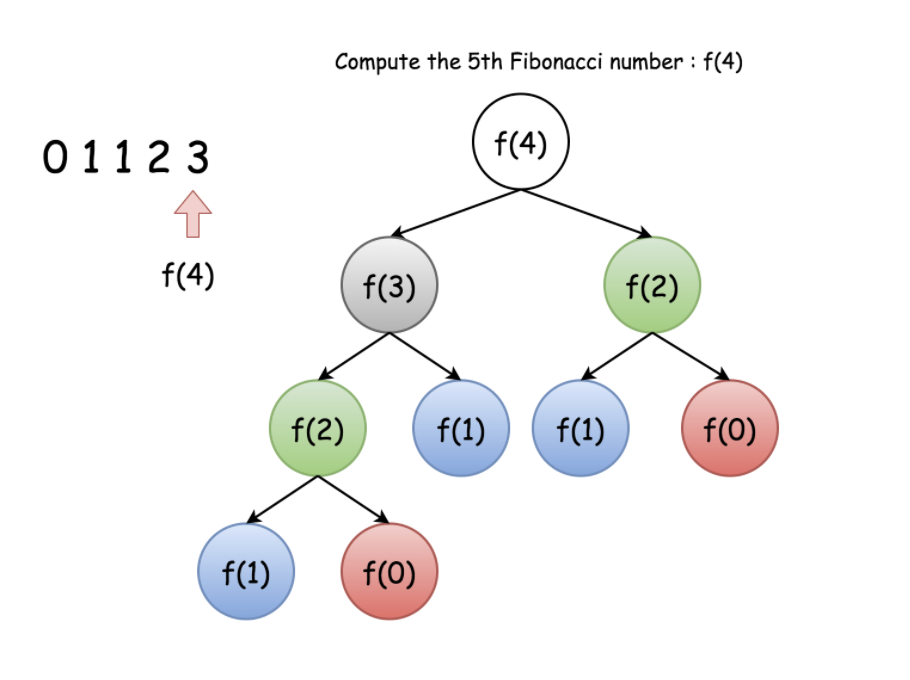
In order to eliminate the duplicate, we would have to store the intermediate results in the cache in order to use them later without recalculate them when the time comes.
For our example with Fibonacci, we will have to use an HashMap to store the intermediate results of F(n) where the key in the Hashmap is the value n. Below is an example of code of Fibonacci using the HashMap as a cache.

    class Solution {
        Map<Integer, Integer> map = new HashMap<>() {{
            put(0, 0);
            put(1, 1);
        }};

        public int fib(int n) {
            if (map.containsKey(n)) return map.get(n);
            int result = fib(n - 1) + fib(n - 2);
            map.put(n, result);
            return result;
        }
    }

Complexity analysis

Time complexity

In order to understand how your algorithm is performing, you will need to calculate the complexity for your recursion.
Given a recursion algorithm, its time complexity O(T) is typically the product of the number of recursion invocations (denoted as R) and the time complexity of calculation (denoted as O(s)) that incurs along with each recursion call:
O(T) = R ∗ O(s)

Print a string in reverse order

In the problem of reversing a String, A recurrence relation can be expressed as follows:
printReverse(str, 0, n) = printReverse(str, 1, n) + print(str[0]).
As you can see, the function will be recursively invoked n times, where n is the size of the input string. At the end of each recursion, we simply print the leading character, therefore the time complexity of this particular operation is constant , ie O(1).
To sum up, the overall time complexity of our recursive function printReverse(str, 0, n) would be O(printReverse) = n * O(1) = O(n).

Execution tree

For recursive functions, it is rarely the case that the number of recursion calls happens to be linear to the size of the input. For instance, let consider the case of Fibonacci series. The recurrence relation is defined as F(n) = F(n-1) + F(n-2). It does not seem straightforward to calculate the number of recursion invocations during the execution of the Fibonacci function.

In this case, it is better resort to the execution tree, which is a tree that is used to denote the execution flow of a recursive function in particular. Each node in the tree represents an invocation of the recursive function. Therefore, the total number of nodes in the tree corresponds to the number of recursion calls during the execution.

The execution tree of a recursive function would form an n-ary tree, with n as the number of times recursion appears in the recurrence relation. For instance, the execution of the Fibonacci function would form a binary tree, as one can see from the following graph which shows the execution tree for the calculation of Fibonacci number F(4).

In a full binary tree with n levels, the total number of nodes would be 2^n - 1. Therefore, the upper bound (though not tight) for the number of recursions in f(n) would be 2^n -1, as well. As a result, we can estimate that the time complexity for F(n) would be O(2^n).

Memoization

Previously, we discussed the technique of memoization that is often applied to optimize the time complexity of recursion algorithms. By caching and reusing the intermediate results, memoization can greatly reduce the number of recursion calls, ie reducing the number of branches in the execution tree. One should take this reduction into account when analyzing the time complexity of recursion algorithms with memoization.

Let's get back to our example of Fibonacci number. With memoization, we save the result of Fibonacci number for each index n. We are assured that the calculation for each Fibonacci number would occur only once. And we know, from the recurrence relation, the Fibonacci number F(n) would depend on all n-1 precedent Fibonacci numbers. As a result, the recursion to calculate F(n) would be invoked n-1 times to calculate all the precedent numbers that it depends on.

Now, we can simply apply the formula we introduced in the beginning of this chapter to calculate the time complexity, which is O(1) * n = O(n). Memoization not only optimizes the time complexity of algorithm, but also simplifies the calculation of time complexity.

Examples of problems using recursion

Maximum depth of a binary tree

In this problem, you are given a binary tree and you are asked to calculate the maximum depth of the given tree. A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

The base case that we can define here is when the given tree is empty. That means of the root == null. In this case, we just have to return 0.
Now we are thinking about the recursion relation. In the otherwise case, we should assume that we have at least the root as a node and eventually a left subtree and a right subtree. So that means, we need to count the root node as 1 in the maxDepth of the global tree and then add the maximum between the max depth of the left subtree and the max depth of the right subtree. This gives us the below code.

    class Solution {
        public int maxDepth(TreeNode root) {
            if (root == null) return 0;
            return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
        }
    }

Conclusion

In this article, we focused of the main concept of recursion. Recursion is a beautiful concept in Software programming. With the recursion, we can write simple, beautiful and elegant code to solve complex problems.
We discussed the general workflow to solve a recursion problem. One needs to define the recursion function, write down the recurrence relation and the base case. Sometimes to improve the time and space complexity, one needs to incorporate the memoization that consists of storing the intermediate results in order to reuse them late when need be.

References

Most of the credit of this article should be given to Leetcode. https://leetcode.com/explore/featured/card/recursion-i/

---